Self-stabilizing Systems in Spite of Distributed Control. A review.

Self-stabilizing Systems in Spite of Distributed Control, Edsger W. Dijkstra, 1974.

All computer science students know Dijkstra’s algorithm for finding the shortest path between two nodes in a graph, but Dijkstra’s contributions to the field of computer science cannot be summed up in a single algorithm, nor can I do justice to all of it in a single blog post. Instead, today I’ll be looking at his seminal work on self-stabilisation. This was the paper that earned him the ACM PODC Influential-Paper Award (later renamed to the Dijkstra award in his honour).

It’s a really neat algorithm, and the paper covers an amazing amount of ground in two pages. So much ground that I’ll only discuss his k-state solution for the self-stabilising token ring problem in this post.

But why

Why do we bother about self-stabilisation? Self-stabilisation implies that something has gone wrong that we’re trying to recover from, but shouldn’t we aim for fault-tolerance where nothing ever goes wrong? It isn’t always possible (and perhaps it’s a little naive) to ensure that a system is completely fault-tolerant. Malicious actors exist, hardware and power failures happen, bits can randomly flip¹. Rather than play whack-a-mole with all the problems that could potentially occur, a system that monotonically tends towards correctness has some appeal.

During a recent reading group discussion on the CAP Theorem, one of my friends talked about the difficulty of recovering from a partition. The problem is that we often reason about distributed systems inductively: the current state is correct because we make a non-breaking move from a correct previous state to the current state. But if operations aren’t sufficiently limited during a partition, then certain invariants may no longer hold after a partition heals, and we can no longer perform the inductive step. Having a self-stabilising (i.e. self-healing) system, would allow a system to reconcile errors from a partition.

The problem

Dijkstra kicks us off by discussing the task of synchronising “loosely coupled cyclic sequential processes”. One way to think of this is an operating system coordinating processes that are running concurrently. To ensure that “the system is in a legitimate state”, processes must run only when they are allowed to. If there is some mechanism to centralise control, then this is trivial. Having a single leader is always unambiguous. For example, if there is some shared memory protected by mutual exclusion, then each process could simply check the shared memory for permission to run.

Now, Dijkstra introduces the complication of distributed control — consider a scenario where:

1. There is no universally shared state
2. Each process can only communicate with a limited number of other processes

(1) means that there is no centralised control mechanism, and (2) means that only local information is available at any point in time. As Dijkstra puts it: “local actions taken on account of local information must accomplish a global objective”. This is what he means by distributed control.

To formalise the problem a bit, Dijkstra tells us to consider a ring of nodes, where each node has a finite state machine. Now consider that each machine is allowed to hold a “privilege”² (i.e. a token, or a mutual exclusion) that allows it to “move” (i.e. let the process run).

There are 4 criteria for a legitimate state in this system:

1. At least one privilege must be present (i.e. at least one process holds the mutex)
2. Only legitimate states are reachable from a legitimate state (i.e. we cannot degrade)
3. Each privilege must be present in at least one legitimate state (i.e. legitimate states do not lead to the starvation of a machine)
4. Any legitimate state is reachable from any other legitimate state in a finite number of steps

And now we get the definition of a self-stabilising system as one that, regardless of the initial state eventually finds itself in a legitimate state in a finite number of moves (convergence). Additionally, by rule (2), this system is also guaranteed to stay in a legitimate state afterwards (closure).

The solution

Dijkstra’s solution relies on a tiny bit of asymmetry. Consider a setup with N+1 machines labelled from 0 to N, and let the 0th machine be called the “bottom machine” (the Nth machine is called the “top machine”).

Now, let each machine keep track of its state S with 0 <= S < K, where K > N. This ensures that there are at least as many states as there are machines. And let L refer to the state of the machine on the left.

For the bottom machine, if L = S then the machine has the mutex, and after moving it sets S := (S+1) mod k.

For all other machines, if L != S then the machine has the mutex, and after it moves it sets S := L.

Here’s a 4-ring example:

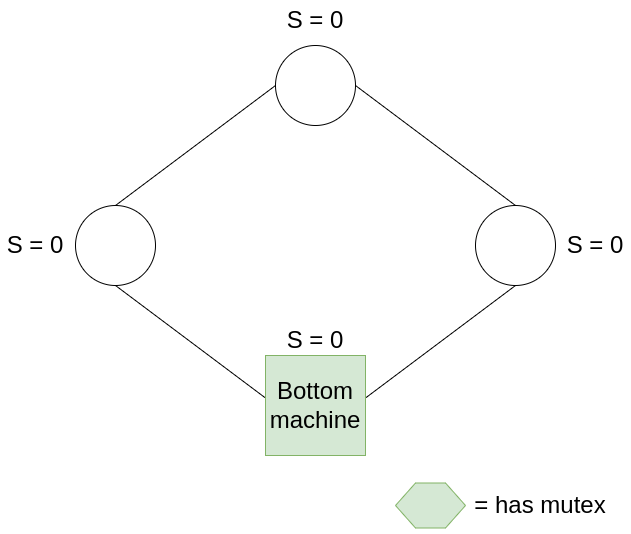
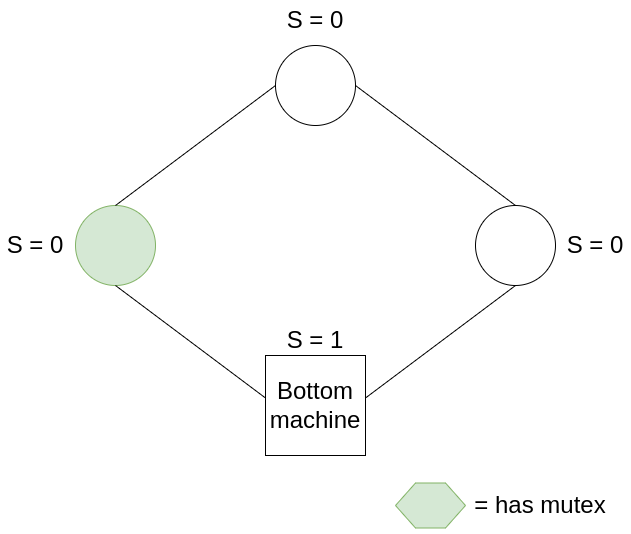
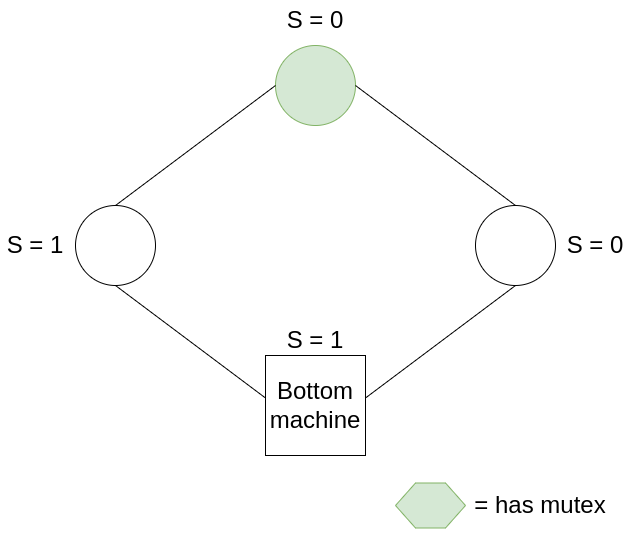
In this example, all machines have S = 0, hence the mutex belongs to the bottom machine. After the bottom machine moves, it sets S = S + 1, i.e. S = 1, passing on the mutex to the next machine. The mutex continues to be passed around the ring in this manner.

Proof sketch

To show that this system is self-stabilising, we’ll show the following:

• A system in a legitimate state always remains in a legitimate state (closure)
• There can never be 0 mutexes (because that would be game over, no progress can be made)
• The number of mutexes never increases
• If the number of mutexes is greater than 1, the system will always eventually reduce the number of mutexes (convergence)

The first property is easy to show. Given that the system is in a legitimate state, one and only one machine has the mutex. If it’s the bottom machine, then all other machines must have the same state s as the bottom machine. After the bottom machine consumes its mutex, it increases its state to s+1, which produces exactly one mutex that belongs to the machine on its right.

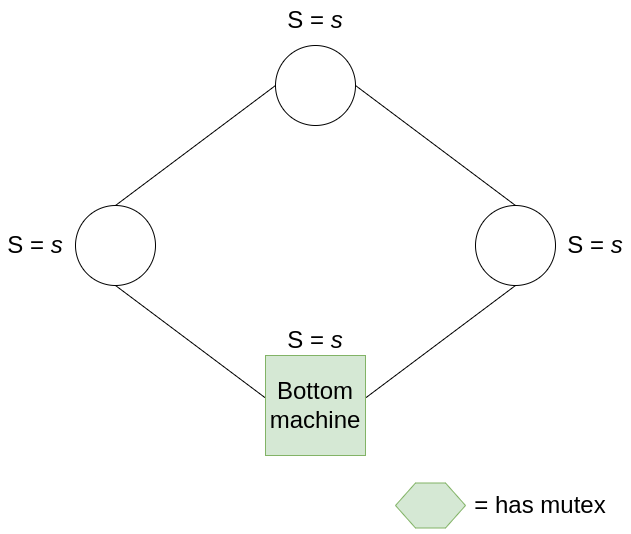
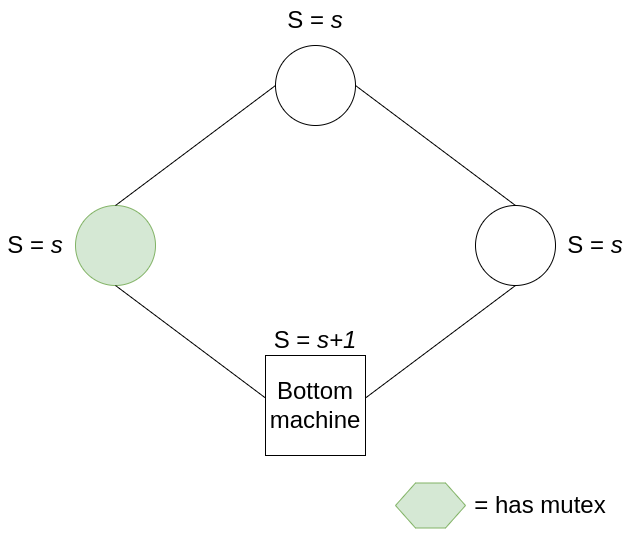
If, instead, the only mutex belongs to one of the other machines, then we need to examine its state. Let’s say this machine has state s, and its left neighbour has state s’ such that s != s’ (the criterion for owning the mutex). All machines to the right of this machine, up to the bottom machine, must share state s (otherwise there will be more than one mutex); and all machines from the bottom machine up to this mutex-owning machine must have state s’. Thus, when this machine consumes its mutex, it changes state to s’, and produces exactly one mutex for the machine on its right. In this way, mutexes pass in an orderly fashion around the ring.

---

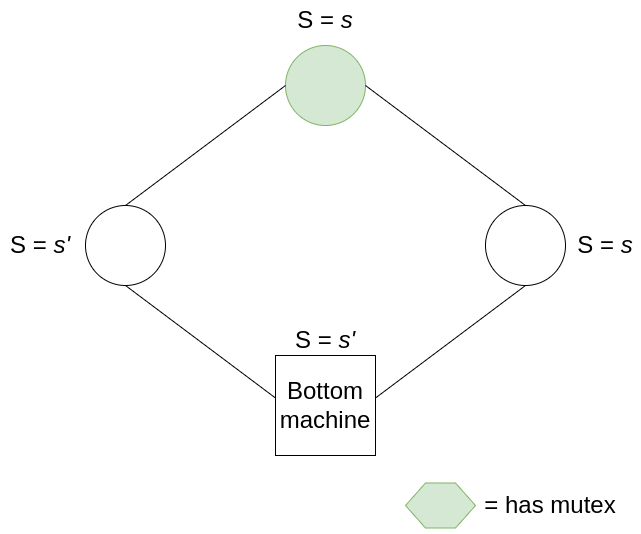
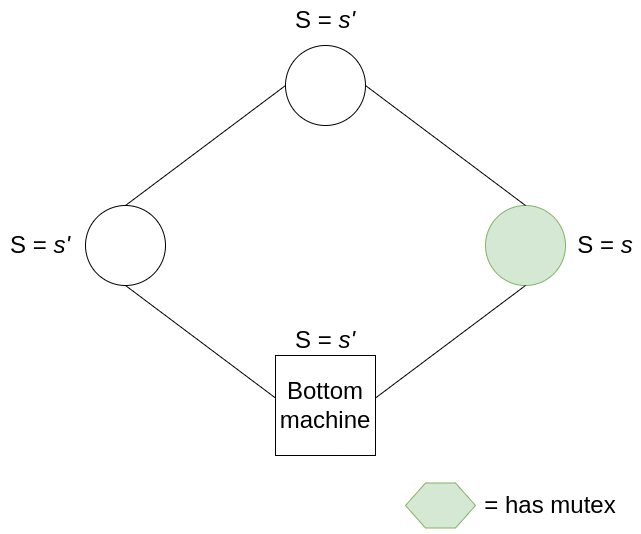
Let’s now show that there can never be 0 mutexes. Here we see how Dijkstra’s little bit of asymmetry comes in to save the day. We first assume that there are no mutexes in the system. This means that all non-bottom nodes have the same state as its left neighbour. Let’s call this state s. Now let’s consider the bottom node’s state (let it be labelled t). For the node on the right of the bottom node to not have the mutex, it must be that s = t. However, the node to the left of the bottom node has state s, hence for the bottom node to not have the mutex, it must be that t != s. We thus have a contradiction, and have to reject our initial assumption that there are no mutexes in the system.

---

We can also show that the number of mutexes never increases. Whenever a machine makes a move, it only changes its state. And for all machines, determining whether the machine owns a mutex depends only on its state plus the state of its left neighbour. Hence, a machine that consumes a mutex can only produce a mutex for its right neighbour. If this doesn’t happen, then the number of mutexes decreases (but we’ve already shown it can never decrease to 0); and if a mutex is produced, the number of mutexes simply remains the same. In no scenario can the number of mutexes increase.

---

For the last part, we have to show that the system converges to a legitimate state. Let us say that the system has h mutexes, where h > 1. This is easy to imagine:

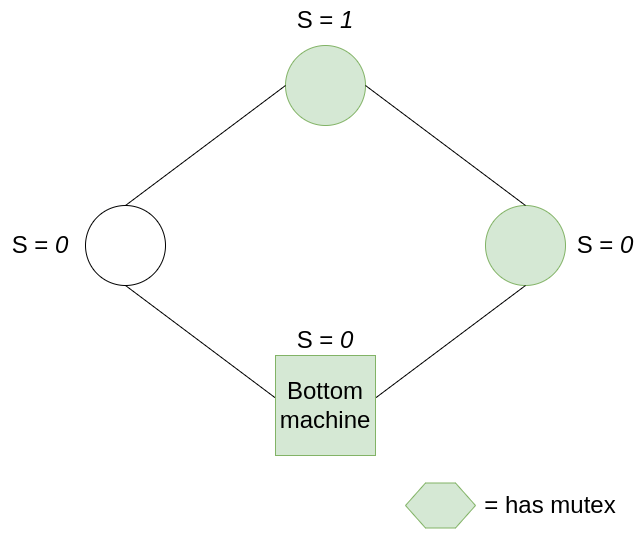
In order for the system to not converge, whenever a mutex is consumed, it has to produce another mutex. Let’s consider non-bottom nodes first. For this scenario to happen, a node holding the mutex must have it such that the node to its right doesn’t have a mutex. If this is not the case, then after this turn, the number of mutexes necessarily decreases by 1 or 2.

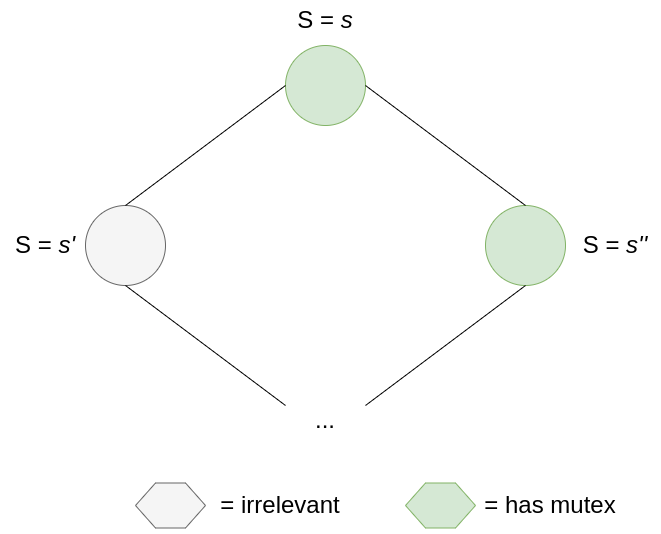
So, to preserve the number of mutexes, consuming a mutex must produce a mutex for the node on the right.

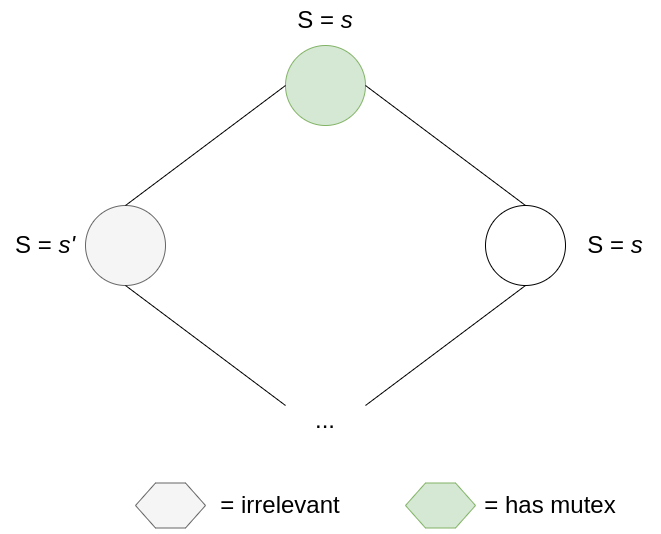
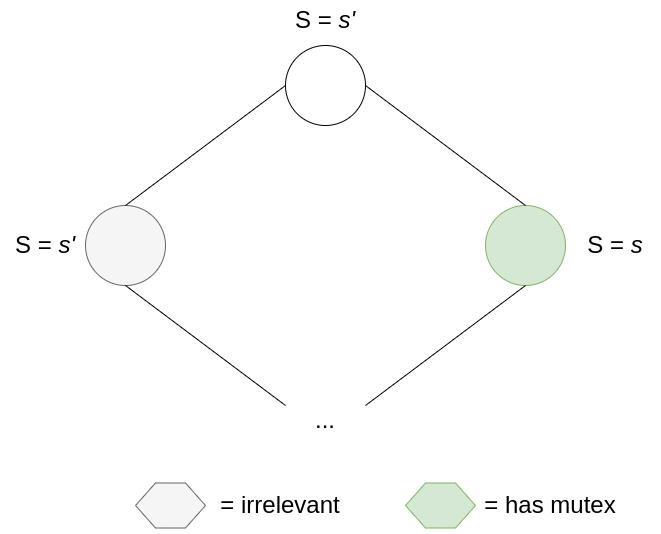
This means that even if the number of mutexes doesn’t decrease, mutexes will consistently move towards the right of the ring and eventually reach the bottom machine:

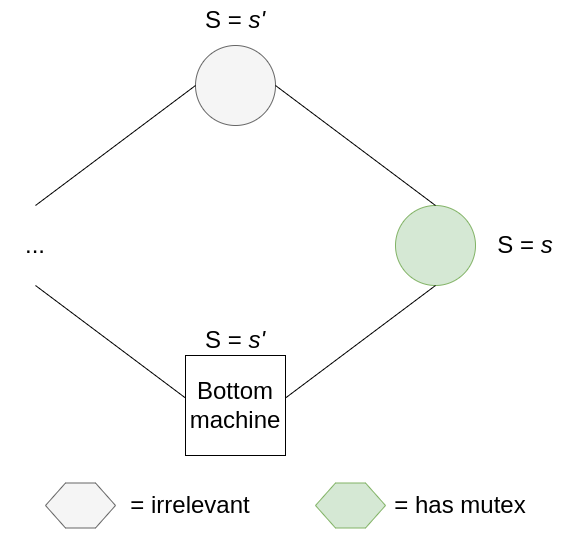
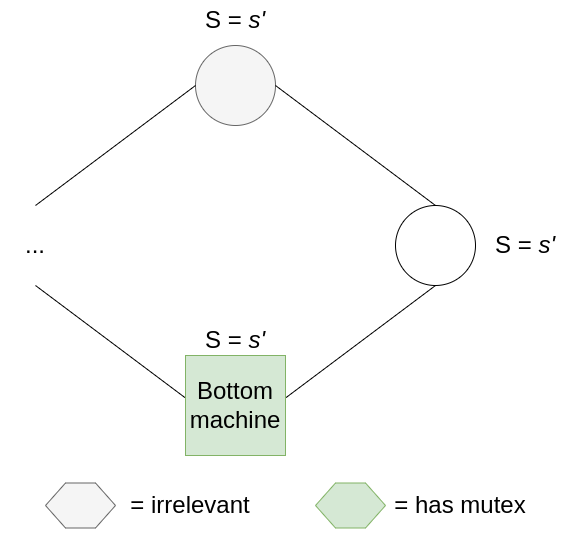
Here’s where the magic comes in. Eventually, non-bottom nodes will not be able to move without destroying a mutex (maybe all the mutexes are bunched up to the right of the ring, so collisions are unavoidable), so the bottom node will have to move instead. It’s still entirely possible to maintain the number of mutexes here, but the bottom machine’s state will now go from s to s+1(mod k). Like a ratchet, the bottom node will eventually cycle through all k possible states. Combine this fact with the pigeon-hole principle: we have at least N+1 states and N+1 nodes, so there is at least one state that is not inhabited by any other node at any point in time. Eventually, the bottom node will acquire a unique state, and it will not own the mutex until this unique state is copied one-by-one starting from the node on its right until it reaches the node to its left. By the time this happens, the ring is reset (because non-bottom nodes can never introduce new states, they can only copy states from their left neighbours), and we enter the legitimate state previously discussed where all nodes share the same state.

The bottom node acts like a dam, and once it spills, its purifying water steadily and surely washes over the other nodes in the system until the inconsistencies are flushed out.

Closing thoughts

It’s beautiful to see how this algorithm works in action. Before I understood it properly, I tried to systematically go through all the possibilities to make the algorithm fail, but as we saw above, this is not possible.

What really irks me, however, is the fact that the system continues acting while in an illegitimate state. In other words, at some point, it’s possible to have multiple mutexes at once. Damage is contained because this situation doesn’t persist, but some pretty nasty things can happen in the meanwhile. I’ll need to follow up with other work done in self-stabilisation to see how this is dealt with in practice.

1. No, really. This paper measured memory errors in a large fleet of commodity servers, and found that a third of their machines saw at least one error per year. Rare, but much more frequent than I had expected.
2. Technically, Dijkstra says one or more privileges, but for the sake of simplicity let’s consider only a single privilege.